閏年をめぐって2
グレゴリオ暦でも閏の問題は完全に解決したわけではなく3320年につき1日ずれます。1923年,それまでユリウス暦を使っていたギリシャ正教会などは改訂ユリウス暦と呼ばれる新しい暦を制定しました。
1)西暦年が4で割り切れる年は閏年
2)ただし,西暦年が100で割り切れる年は平年
3)ただし,西暦年を900で割った余りが200または600になる年は閏年
1)と2)はグレゴリオ暦と同じですが,3)は違っています。これによると閏年は900年間に900/4-900/100+2=218回ありますから,1年は平均
365+218/900=365.242222
日で,グレゴリオ暦より1桁も精度がよく,数万年もずれません。将来,2800年がグレゴリオ暦では閏年なのに対し,改訂ユリウス暦では平年になり,日付は1日ずれます。2900年は逆に改訂ユリウス暦だけが閏年となり,日付は再び一致しますが,3200年と3300年でまた同じようなことが起こります。正確ではあってもかえって複雑ですから,果たしてどこの国が使っているかは知りません。
このような新しい正確な暦は簡単にできます。i 年の間に j 回閏年を置くと1年の平均日数は365 + j/i 日であり,それが1回帰年 365.242194・・・日に近くなるような自然数 i と j を探していきます。1000年間にわたって調べた結果が下表です。
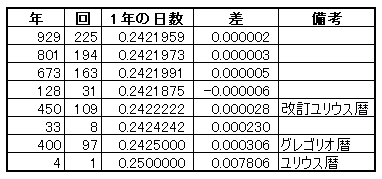
第1列は i,第2列は j であり,第3列は j/iの値,第4列は0.242194との差です。第3列の値が0.242~0.243となるものは1000年間に499回ありますが,そのベスト3件と参考5件を載せました。最も誤差が小さいのは閏年を929年間に 225回設ける場合ですが,これを実際に設置することは困難であり無意味です。2番目3番目についても同様のことがいえます。それらに比べると誤差はやや大きいが,上記の改訂ユリウス暦よりは数倍精度のよい,4番目の場合,128年間に31(=128/4-1)回の閏年とは
1)西暦年が4で割り切れる年は閏年
2)ただし,西暦年が128で割り切れる年は平年
とすれば使えそうですね。128で割り切れるとは3回続けて4で割った時の商が偶数であるということです。では実際に改暦が行われたら・・・近い将来の変更は 1)より2100年は閏年で,2)より2048年は平年となります。
では6番目の場合の閏年設置法を考えてみましょう。なおこれらの表値を求めるにはここを
