優劣の差は？
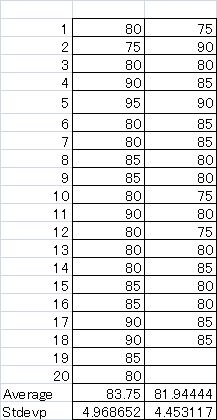
ttest1.jpg(28247 byte) 　左の表を見てください。AクラスとBクラスの試験の結果です。Aクラス20人の平均点は83.75点， Bクラス18人の平均点は81.94点。これだけ見るとAクラスの方が優れているようですが，果してそういえるでしょうか？ 平均±標準偏差の範囲はAクラスでは 78.78〜88.72，Bクラスでは77.49〜86.40 となって範囲は重複しています。
この2クラスの成績に違いがあるかどうかを調べるにはｔ検定の手法を使います。 それには検定の常套手段として「2クラスの成績に違いはない」という帰無仮説を立て，それが起こる確率を計算し, もし5％以下ならその仮説を棄却するという方法をとります。
その確率は　=ttest(データ範囲1,データ範囲2，n，m ）
ただし　片側検定なら　n=1，　 両側検定なら　n=2
対をなすデータの時は m=1，　等分散の 2 標本を対象とする時は m=2 ，　非等分散の 2 標本を対象とする時には m=3
今の場合は n=m=2 とすればよろしい。そうするとこの確率は0.26となります。 したがってこの帰無仮説は棄却できない，すなわち両クラスの成績に差異がないとは認められない，よく 起こることなのです。

ttest2.jpg(24942 byte) 　次に右の表は10人の患者に薬を投与する前と後で検温した結果です。この薬は効果があったのでしょうか？平均値だけ見ると違いはないようですね。
投薬前後の体温には差異がないという帰無仮説を同じようにして検定します。 この場合はn=2　m=1　とします。すると その確率は0.044,この値は0.05より小さいので帰無仮説は棄てられる，すなわち差異は認められることになります。しかし積極的にそう言わずに投薬前後で差異がないという帰無仮説は棄てられると言う習慣になっています。 上の例との一番の違いは各行データは各個人に割り当てられ固定されているということです