PC揤暥嫵嵽亂2亃丂丂働僾儔乕偺朄懃偺棟夝丂丂
亂3亃
嶌壴堦巙丂乽揤暥嫵堢乿丂9寧崋丂2005丂丂丂
1. 働僾儔乕偺朄懃
丂揤暥壆側傜偩傟偱傕抦偭偰偄傞働僾儔乕偺朄懃偩偑丆偙傟傪偒偪傫偲愢柧偡傞偺偼旕忢偵擄偟偄丅
嘥乯榝惎偼懢梲傪堦偮偺徟揰偲偡傞懭墌婳摴傪昤偔丅
嘦乯懢梲偲榝惎傪寢傇慄暘偲懭墌偺挿幉偲偱偱偒傞愵宍偺柺愊懍搙偼堦掕偱偁傞丅
嘨乯偳傫側榝惎偱傕岞揮廃婜偺俀忔偲婳摴挿敿宎偺俁忔偺斾偼堦掕偱偁傞丅
偲偄偆暥復偩偗偱撪梕傪棟夝偡傞偙偲偼柍棟偵嬤偄偟丆偙偺審傪埫婰偟偰傕傎偲傫偳柍堄枴偱偁傞丅
傑偢丆戞侾朄懃偵偍偄偰懭墌偲偼
丂丂丂丂x2乛a2亄y2乛b2亖1
偲偄偆幃偱昞偝傟傞嬋慄偲偄偆傛傝乽墌傪偁傞堦曽岦偩偗偵埑弅偟偨傕偺乿偲峫偊偨傎偆偑傢偐傝傗偡偄丅敿宎 a 偺墌傪 倷曽岦偩偗偵 b乛a 攞偡傞偲挿敿宎 a丆抁敿宎 b 偺懭墌偑摼傜傟傞丅懭墌偺宍偼 a 偲 b 偲偄偆戙傢傝偵丆a 偲棧怱棪 e亖併(a2亅b2乯乛a 偲偱摿挜偯偗傜傟傞偲偡傞乮塃恾乯丅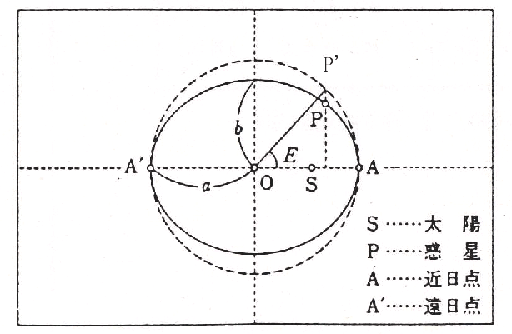 倕偼0埲忋1傛傝彫偝偄抣傪偲傝丆0偺偲偒偵偼墌傪丆侾偵嬤偔側傟偽側傞傎偳滸暯側懭墌傪昞偡偙偲偼梕堈偵傢偐傞丅懭墌偺徟揰偼乮亇ae丆0乯偱偁傝丆戞侾朄懃傛傝懢梲偼堦偮偺徟揰俽乮ae丆0乯偵丆榝惎偼懭墌忋俹乮X丆Y乯偵埵抲偟偰偄傞丅尨揰傪拞怱偲偟敿宎倎偺墌傪昤偒丆偦偺墌廃忋偵俹'傪恾偺傛偆偵掕傔偰佢俹'俷倃亖俤傪棧怱嬤揰妏偲偄偆丅
倕偼0埲忋1傛傝彫偝偄抣傪偲傝丆0偺偲偒偵偼墌傪丆侾偵嬤偔側傟偽側傞傎偳滸暯側懭墌傪昞偡偙偲偼梕堈偵傢偐傞丅懭墌偺徟揰偼乮亇ae丆0乯偱偁傝丆戞侾朄懃傛傝懢梲偼堦偮偺徟揰俽乮ae丆0乯偵丆榝惎偼懭墌忋俹乮X丆Y乯偵埵抲偟偰偄傞丅尨揰傪拞怱偲偟敿宎倎偺墌傪昤偒丆偦偺墌廃忋偵俹'傪恾偺傛偆偵掕傔偰佢俹'俷倃亖俤傪棧怱嬤揰妏偲偄偆丅
丂丂X 亖 a cos E 丂丂丂 丂乮侾乯
Y 亖 b sin E
丂丂亖 a併(1亅e俀) sin E 丂乮俀乯
偡傞偲懢梲榝惎娫嫍棧俽俹偼
倰 亖併((X 亅 ae)俀 + Y俀)
亖 a ( 1 亅 e cos E) 丂乮俁乯
偲彂偗傞丅倰偺嵟戝抣丆嵟彫抣偼師偺傛偆偵梌偊傜傟傞丅
丂丂丂嵟彫抣丂a乮侾亅e乯丂E亖0並丂丂 丂丂俹偑俙偵堦抳偡傞偲偒
丂丂丂嵟戝抣丂a乮侾亄e乯丂E亖180並丂丂丂俹偑俙'偵堦抳偡傞偲偒
俙傪嬤擔揰丆俙'傪墦擔揰偲屇傇栿偼帺柧偱偁傠偆丅a 偼 倰 偺嵟戝抣偲嵟彫抣偺暯嬒偲側傞偺偱暯嬒嫍棧偲傕尵傢傟傞丅榝惎偑懭墌忋傪偳偺傛偆偵塣摦偟丆偄偮偳偙偵偄傞偐師偺働僾儔乕偺曽掱幃乮係乯偱梌偊傜傟傞丅偙傟偼戞俀朄懃乽柺愊懍搙偼堦掕乿偐傜摼傜傟傞偑丆偦偺摫弌偵偼偐側傝偺擡懴椡偑梫傞丅弮椡妛揑側昞尰偱偼乽妏塣摦検偑曐懚偝傟偰偄傞乿偲側傞丅
丂丂E 亅e sin E = M丂丂丂丂丂 (係)
丂丂丂M = n t丂丂丂丂丂丂丂丂乮俆乯
M 偼暯嬒嬤揰棧妏偲尵傢傟丆嬤擔揰捠夁帪偐傜偺宱夁擔悢倲偵斾椺偟丆嬤擔揰捠夁帪偵0丆墦擔揰捠夁帪偵
兾偲側傞丅働僾儔乕偺曽掱幃偺夝偼
丂丂丂丂丂倷亖 e sin 倶丂
丂丂丂丂丂倷亖倶 亅M丂
偺岎揰偱偁傝丄0亝e亙1偱偁傞偐傜昁偢夝偼1屄偩偗懚嵼偡傞丅偟偐偟夝愅揑偵偼夝偗側偄偺偱丄M乮儔僕傾儞乯偲 e 傪梌偊偰悢抣揑偵夝偔傢偗偩丅媮傑偭偨俤傪乮侾乯丆乮俀乯偵戙擖偟偰倃丆倄偑媮傑傝丆偦偺帪偺榝惎偺埵抲偑摼傜傟傞丅
戞侾丆戞2朄懃偼侾偮偺榝惎偵偮偄偰偱偁傞偑戞俁朄懃偼暋悢屄偺榝惎偵偮偄偰偺婰弎偱偁傞丅岞揮廃婜 p 偲暯嬒嫍棧 a 偺娭學偼
丂丂丂丂丂a3亖GM p2乛(4兾2)丂丂丂丂丂丂乮俇乯
M偼懢梲偲榝惎偺幙検榓偱偁傞偑懢梲偺幙検偲偟偰嵎偟巟偊側偄丅p丆a丆M 偺扨埵傪擭丆揤暥扨埵丆懢梲幙検偲偡傞偲丆戞俁朄懃偼師偺傛偆偵旕忢偵娙扨偵昞偝傟傞丅
丂丂丂丂丂a3亖p2
乮俆乯偺斾椺掕悢値偼暯嬒擔乆塣摦偲偄傢傟榝惎偑侾擔摉偨傝岞揮塣摦偡傞妏搙偱暯嬒妏懍搙偵摉偨傞丅
丂丂丂丂丂 n = 360乛(365.24219p)
丂丂丂丂丂丂丂= 0.985647365 a亅侾丏俆
偲彂偗傞丅懢梲偵嬤偄榝惎傎偳値偼戝偒偔丆懍偔岞揮偟偰偄傞丅
2.椺戣偲夝朄
丂偱偼偙傟傜傪僷僜僐儞偱幚廗偟偰傒傛偆偲偄偭偰傕丆傑偢懭墌傪昤偔偙偲偐傜偟偰戝曄偱偁傞丅乮侾乯乮俀乯偵偍偄偰 a 偲 e 偺悢抣傪梌偊偰乮倃丆倄乯傪僾儘僢僩偡傟偽偄偄偺偩偑Excel偱傗傠偆偲偡傞偲懭墌偺宍偼惓妋偱偼側偄丅働僾儔乕偺曽掱幃乮係乯偺夝朄偼悢抣寁嶼偺弶曕揑側墘廗栤戣偱丄Excel偱夝偗傞偑丆偦偺屻偺僌儔僼昤夋偼戝曄偩丅偦傟側傜偄偭偦慡晹傪枮偨偡僾儘僌儔儉傪嶌傟偽偄偄偺偩偑丆挿帪娫偺帋峴嶖岆傪妎屽偟側偗傟偽側傜側偄丅偦偙偱昁梫偵墳偠偰昅幰偺僒僀僩[1]傛傝幚峴僼傽僀儖傪僟僂儞儘乕僪偟偰偍巊偄偔偩偝偄丅俁偮偺朄懃傪價僕儏傾儖偵棟夝偟傛偆偲偄偆傕偺偱丆恾2偼戞2朄懃偵偮偄偰偺恾愢偱偁傞丅榝惎乮愒嬍乯偑懢梲偵嬤偄偲偒偼懍偔丆墦偄偲偒偼備偭偔傝偲婳摴忋傪塣摦偡傞丅
偙偙偱偼Excel偱偱偒傞俀偮偺椺戣傪夝偄偰傒傛偆丅
| 椺1丂崱擭尦擔偺抧媴懢梲娫嫍棧傪媮傔傛丅傑偨崱擭偺嬤擔揰捠夁擔偲墦擔揰捠夁擔傪媮傔傛丅
|
丂棟壢擭昞偵傛傞偲抧媴偺婳摴梫慺偼
丂丂丂a=1丆丂e=0.00167丂
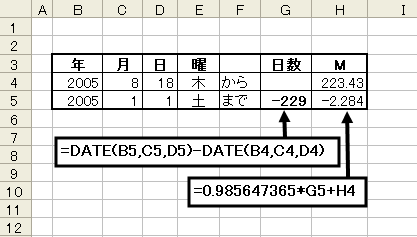
偱偁傝2005擭8寧18.0擔偵偍偄偰M=223.429亱偱偁傞丅1寧1擔偼229擔慜偱偁傞偐傜丆尦擔偱偼
M=-2.284亱偲側傞乮壓恾嵍乯丅側偍帪崗偼倀俿亖0h偡側傢偪俰俽俿亖9h偵偍偗傞抣偱偁傞丅
偙偺M傪儔僕傾儞偵曄姺乮娭悢radians乯偟偰乮係乯傪夝偔偲
丂丂丂E亖亅0.04054丂偱偁傝
丂丂丂X亖0.982478183丂丂Y亖亅0.040527772丂丂丂r亖0.983313724丂丂偑摼傜傟傞乮壓昞乯丅
偙偙偱偼僯儏乕僩儞朄傪梡偄偰丂x2亖x1亅倖(x1)乛倖'(x1) 偲寁嶼偟偨丅
偨偩偟 f(x)亖倶亅倕sinx亄俵丂丂丂丂 f'(x)亖侾亅倕cosx
M偺抣偑侽偵嬤偄偺偱丆尦擔偵抧媴偼嬤擔揰偺嬤朤偵偄傞偼偢偩丅壓恾嵍偺僔乕僩偵偍偄偰1寧3擔偵偼 M亖亅0.313亱偱丄1寧4擔偵偼 M亖0.0117亱偱偁傞偐傜嬤擔揰捠夁擔偼1寧4擔偱偁傞偙偲偑傢偐傞丅摨條偵偟偰 M亖180亱偲側傞擔傪扵偡偲丆墦擔揰捠夁擔偼7寧5擔偱偁傞偙偲偑傢偐傞丅
 丂
丂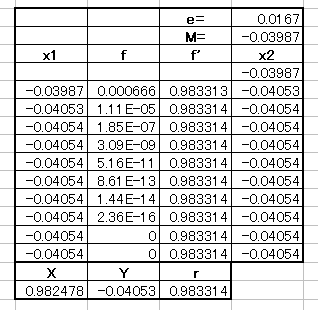
| 椺俀丂栘惎偲揤墹惎偺塹惎偺婳摴挿敿宎偲岞揮廃婜偺懳悢僌儔僼傪昤偗丅偦傟偧傟捈慄忬偵暲傇偑丆偦偺岡攝偲愗曅偺堄枴傪峫嶡偣傛丅
|
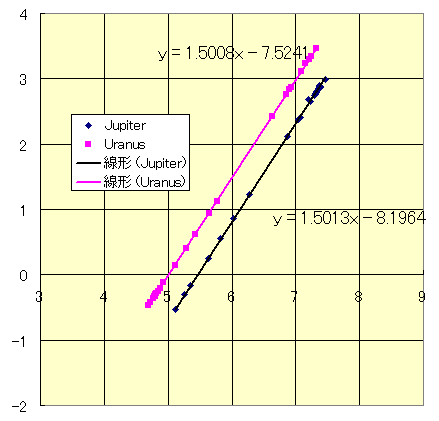 丂[2] 偵嵹偭偰偄傞栘惎62屄丆揤墹惎24屄偺塹惎偺婳摴挿敿宎 a (km)偲岞揮廃婜 p (day)偺僨乕僞傪巊偄偦偺懳悢傪僾儘僢僩偟偨丅
揰楍偑捈慄忬偵暲傇偲偄偆偙偲偼
丂[2] 偵嵹偭偰偄傞栘惎62屄丆揤墹惎24屄偺塹惎偺婳摴挿敿宎 a (km)偲岞揮廃婜 p (day)偺僨乕僞傪巊偄偦偺懳悢傪僾儘僢僩偟偨丅
揰楍偑捈慄忬偵暲傇偲偄偆偙偲偼
丂丂丂丂丂p亖俠亊a兛
偲偄偆偙偲傪堄枴偡傞丅兛偼偙偺捈慄偺孹偒偱1.5偱偁傝(俇)偲堦抳偡傞丅傑偨愗曅偼
丂丂丂丂丂俠亖10-8.1964亖6.36209E-09乮栘惎乯
丂丂丂丂丂丂亖10-7.5241亖2.99158E-08乮揤墹惎乯
偱偁傞偑乮俇乯傛傝 俠亖俀兾乛併乮GM乯偱偁傞偼偢偩丅幚嵺丆椉榝惎偺侾乛俠俀偺斾偼0.045偱偁傝幙検斾偲堦抳偡傞丅偙偺傛偆偵偟偰丆壩惎偐傜奀墹惎傑偱偺幙検斾偑媮傑傞丅
嶲峫暥專
[1]丂嶌壴堦巙 http://www.kcg.ac.jp/kcg/sakka/uchu/c/sample/kepler.exe
[2]丂JPL http://ssd.jpl.nasa.gov/
 倕偼0埲忋1傛傝彫偝偄抣傪偲傝丆0偺偲偒偵偼墌傪丆侾偵嬤偔側傟偽側傞傎偳滸暯側懭墌傪昞偡偙偲偼梕堈偵傢偐傞丅懭墌偺徟揰偼乮亇ae丆0乯偱偁傝丆戞侾朄懃傛傝懢梲偼堦偮偺徟揰俽乮ae丆0乯偵丆榝惎偼懭墌忋俹乮X丆Y乯偵埵抲偟偰偄傞丅尨揰傪拞怱偲偟敿宎倎偺墌傪昤偒丆偦偺墌廃忋偵俹'傪恾偺傛偆偵掕傔偰佢俹'俷倃亖俤傪棧怱嬤揰妏偲偄偆丅
倕偼0埲忋1傛傝彫偝偄抣傪偲傝丆0偺偲偒偵偼墌傪丆侾偵嬤偔側傟偽側傞傎偳滸暯側懭墌傪昞偡偙偲偼梕堈偵傢偐傞丅懭墌偺徟揰偼乮亇ae丆0乯偱偁傝丆戞侾朄懃傛傝懢梲偼堦偮偺徟揰俽乮ae丆0乯偵丆榝惎偼懭墌忋俹乮X丆Y乯偵埵抲偟偰偄傞丅尨揰傪拞怱偲偟敿宎倎偺墌傪昤偒丆偦偺墌廃忋偵俹'傪恾偺傛偆偵掕傔偰佢俹'俷倃亖俤傪棧怱嬤揰妏偲偄偆丅
 丂
丂
 丂[2] 偵嵹偭偰偄傞栘惎62屄丆揤墹惎24屄偺塹惎偺婳摴挿敿宎 a (km)偲岞揮廃婜 p (day)偺僨乕僞傪巊偄偦偺懳悢傪僾儘僢僩偟偨丅
揰楍偑捈慄忬偵暲傇偲偄偆偙偲偼
丂[2] 偵嵹偭偰偄傞栘惎62屄丆揤墹惎24屄偺塹惎偺婳摴挿敿宎 a (km)偲岞揮廃婜 p (day)偺僨乕僞傪巊偄偦偺懳悢傪僾儘僢僩偟偨丅
揰楍偑捈慄忬偵暲傇偲偄偆偙偲偼